Contando los pétalos de las flores de cualquiera de los jardines botánicos de la red Med-O-Med es posible que hayas notado algo inusual, preguntándote: ¿Por qué muy pocas plantas tienen 4 pétalos? o ¿por qué un trébol de 4 hojas es tan difícil de encontrar? Y si sigues observando las plantas te podrías dar cuenta de una recurrencia de los números de pétalos con los términos siguientes: 3, 5, 8, 13, 21, 34 o 55. Los lirios por ejemplo tienen 3 pétalos, las achicorias 21, las margaritas 34 o 55… ¿Son estos números aleatorios?
Para entenderlo comenzamos con un famoso matemático italiano del siglo XIII, Leonardo de Pisa (1170-1250 d.C.), más conocido como Fibonacci, que además de tener una importante función en el Renacimiento de las matemáticas en Europa, descubrió una sucesión que ilustra el estrecho entrelazamiento entre las matemáticas y la naturaleza.
Leonardo de Pisa o Fibonacci
Fibonacci nació en la Republica de Pisa y creció en el norte de África, concretamente en Bugía (Argelia actual), un lugar caracterizado en su momento por su desarrollo económico, cultural y científico.
Su padre ostentaba en la ciudad un puesto diplomático y de comerciante[1] y por ello, desde muy joven, Leonardo estuvo en contacto con el sistema de numeración indo-árabe.
Aprovechó entonces la efervescencia intelectual de Bugía para desarrollar sus conocimientos, estudiando los trabajos de algunos de los eruditos más conocidos del mundo islámico. Entre ellos, los del padre fundador del álgebra, Al-Juarismi, y su famoso tratado, Compendio de cálculo por reintegración y comparación (حساب الجبر و المقابلة).[2]
No obstante, Leonardo no se limitó a estudiar, y viajó también a muchos países del mundo mediterráneo-islámico. Durante estos viajes conoció a numerosos científicos, y poco a poco aprendió los diferentes sistemas de cálculo que utilizaban los comerciantes. De todos los métodos, consideró que el utilizado por los árabes era el más avanzado y el más práctico.[3]
Leyendo, Liber abaci, podemos ver también que contiene la mayoría de los grandes conocimientos en álgebra y aritmética descubiertos por los científicos árabes, como las raíces cuadradas y cúbicas y las ecuaciones de primer y segundo grado.
Al acabar sus viajes, el joven nativo de la República de Pisa regresó a su tierra natal, donde publicó en 1202 una obra, Liber abaci, que lo hizo pasar a la posteridad. Su libro marcó la historia por ser la autoría del primer matemático del mundo occidental en utilizar el sistema de numeración indo-árabe y en compararlo con el sistema romano.
Leyendo, Liber abaci, podemos ver también que contiene la mayoría de los grandes conocimientos en álgebra y aritmética descubiertos por los científicos árabes, como las raíces cuadradas y cúbicas y las ecuaciones de primer y segundo grado.[4] Leonardo participó entonces en este maravillo movimiento de intercambio de conocimientos entre continentes y civilizaciones.
Además, no se conformó con dar a conocer la obra de otros autores, sino que también desarrolló sus propias teorías. Descubrió sobre todo una secuencia recurrente que lleva hoy su nombre: la sucesión de Fibonacci.
La sucesión de Fibonacci
Se trata de una sucesión infinita de números, en la que cada término sucesivo representa la suma de los dos anteriores, de tal manera: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55….
El mito nos cuenta que Leonardo la descubrió estudiando la reproducción de los conejos. Sin embargo, en la realidad la reproducción del animal no sigue esta ley matemática. A pesar de ello, cuando se estudia, se sigue ilustrando esta sucesión con este ejemplo.
Esta secuencia a primera vista parece bastante sencilla, pero tiene un conjunto de propiedades muy impresionantes que nunca han dejado de fomentar la curiosidad y el interés, especialmente, porque aparece recurrentemente en la naturaleza.
La regularidad de los números de Fibonacci en la naturaleza: el ejemplo de la filotaxis
El principal vínculo que veremos aquí entre la sucesión de Fibonacci y la naturaleza se encuentra en lo que se llama en botánica la filotaxis. Esta palabra, de origen griego significa literalmente ordenación de las hojas alrededor de un tallo. En un sentido más amplio, es el estudio de la organización de todos los elementos de una planta, como las semillas, las escamas, las ramas etc.[5] La filotaxis tiene diferentes categorías en función de la disposición de los elementos de la planta, y aquí nos interesaremos solamente en la filotaxis alternada, en la cual se forman espirales que se llaman paristiquios.
¿Cómo se relaciona la filotaxis con la sucesión de Fibonacci?
Los botánicos siempre se habían sorprendido por la regularidad que encontraban en la organización de las plantas, y fue a partir de esa observación que iniciaron una reflexión que les permitió establecer una conexión entre la filotaxis y la secuencia de Fibonacci.
Uno de los primeros en notar una recurrencia en la disposición de las plantas fue el astrónomo y botánico Keppler quien, en el siglo XVII, observó que el número 5 estaba presente con frecuencia en las flores – la flor de la pasión tiene por ejemplo dos niveles de 5 pétalos y de 5 sépalos – así como en las manzanas, que tienen cinco divisiones para sus semillas.[6] Antes de Keppler, el célebre Leonardo Da Vinci identificó también los ciclos de cinco hojas en uno de sus manuscritos: “si tomamos una hoja de referencia, la sexta hoja encontrada en el camino hacia la rama está alineada por encima de la primera, es decir, las hojas están dispuestas en ciclos de cinco”.[7]
La sucesión de Fibonacci tiene un conjunto de propiedades muy impresionantes que nunca ha dejado de fomentar la curiosidad y el interés, especialmente, porque aparece recurrentemente en la naturaleza.
No obstante, hubo que esperar hasta el siglo XIX para relacionar estas observaciones con la sucesión de Fibonacci. Esta conexión fue posible en gran parte gracias al desarrollo de la “filotaxis matemática”, en la cual botánicos y matemáticos juntaron sus investigaciones.[8]
Alexander Braun fue, en 1831, el primero en establecer un vínculo entre el número de espirales (paristiquios) y los términos de Fibonacci a través del ejemplo de las piñas.[9] Sus estudios mostraron que la distribución de las escamas de esta fruta eran siempre dos números consecutivos de Fibonacci (8 y 13 son los más frecuentes).
La hipótesis de Braun, que ilustraba una correspondencia entre los números de paristiquios y la secuencia de Fibonacci, fue comprobada un siglo más tarde por el matemático Alfred Brosseau. En 1968, el matemático realizó un estudio con 4.290 piñas, de diez especies de pinos diferentes de la región de California, y los resultados fueron muy relevantes porque, a la excepción de 74 piñas, todas seguían la sucesión de Fibonacci (¡un 98.3% de coincidencia!).[10] Después de esto, otros estudios siguieron validando este fenómeno.
Podemos también ilustrar esta curiosidad a través del ejemplo de la flor del girasol y la organización de sus semillas en espirales.[11] Solo hay que contar el número de paristiquios en una dirección y después en la otra para darse cuenta de que suelen combinarse de las maneras siguientes: 34-55 / 55-89 / 89-144[12].
Esta lógica se encuentra también con una flor que podemos encontrar en la mayoría de los espacios verdes: las margaritas.
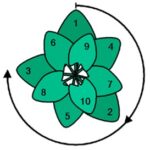
Si nos fijamos en su centro, distinguimos también dos espirales: una en sentido horario y otra antihorario, y resulta que el número de paristiquios en cada sentido sigue también los términos siguientes de la sucesión: 21-34 / 34-55…[13]
Por ejemplo: en la foto de la izquierda podemos ver que la margarita en el sentido horario tiene 34 espirales mientras que, en la foto de la derecha, la misma tiene 21 espirales en el sentido contrario.
¿Todas las flores siguen entonces la secuencia de Fibonacci?
Como se ha expuesto hasta ahora, la organización en paristiquios (espirales) tiene una correspondencia muy alta con los números de Fibonacci. Sin embargo, está relación no se produce cuando la filotaxis no es alternada, sino verticilida (en torno a un mismo tallo) o dística (dispuesta en dos filas verticales opuestas).[14]
¿Por qué se produce, entonces, este fenómeno? Apoyándonos sobre la idea de que las plantas tienen unos colores espléndidos para poder atraer a las abejas u otros animales portadores de polen, podríamos pensar que esta organización tiene un fin utilitarista, conforme a un objetivo concreto. No obstante, la respuesta no es tan sencilla y no existe todavía un consenso real. Los debates continúan, mezclando explicaciones matemáticas, físicas y botánicas, así como algunas místicas o teleológicas.
No obstante, sabemos hoy que en la filotaxis se verifica la ley de divergencia teorizada por el botánico Charles Bonnet, que, en 1754, explicó que: “para cada especie de plantas, el ángulo que forman dos hojas consecutivas, llamado ángulo de divergencia, es constante”[15]. A partir de esta observación, surgieron muchas explicaciones, algunas de las cuales se contradijeron con el paso del tiempo.
Sin ahondar en estos debates académicos, nos interesaremos por el vínculo entre la sucesión de Fibonacci y esta ley botánica. Si observamos la secuencia de Fibonacci, podemos notar que, si dividimos cada número de la secuencia por su predecesor, obtenemos un resultado muy cerca del número Φ, conocido como número áureo.
Son otra vez los botánicos K. Schimper y A. Braun los que observaron en 1831 que la filotaxis espiral estaba asociada, como ya hemos visto, a la secuencia de Fibonacci, pero también al ángulo áureo. Observaron que siempre que se encuentran los términos de Fibonacci, el ángulo de divergencia es equivalente o muy cercano al ángulo de oro o de Fibonacci.[16] Lo llamaron entonces el ángulo de divergencia ideal.
Durante mucho tiempo se ha dicho que este ángulo era ideal en el sentido que permitía a una planta y sus hojas obtener la máxima exposición a la luz del sol, permitiendo también una organización perfecta de las semillas, sin que se dañen una a otra.
Si observamos la secuencia de Fibonacci, podemos notar que, si dividimos cada número de la secuencia por su predecesor, obtenemos un resultado muy cerca del número Φ, conocido como número áureo.
Sin embargo, las teorías más recientes señalan que la necesidad de luz no lleva necesariamente a la planta a adoptar el ángulo de Fibonacci, ya que la iluminación óptima se consigue con mayor frecuencia mediante la producción de hojas largas y delgadas. Esta observación abre, de nuevo, el debate en torno a su explicación.
En conclusión, una cuestión aparentemente tan sencilla como la razón tras la disposición de las hojas en un tallo, o de las semillas, nos ha llevado a ver cómo se unen las matemáticas y la naturaleza, para el deleite de nuestros ojos. El número áureo, según varios pensadores griegos, es una de las razones por las que la naturaleza es tan «agradable y bella» de observar, al igual que ocurre con la arquitectura o la pintura. Esta reflexión nos conduce a una cuestión subyacente, con la que resulta interesante concluir: ¿inventó el hombre las matemáticas o ya estaban presentes en todo lo que nos rodea?
Tristan Semiond – FUNCI
[1] Santiago Miguel Enamorado Báez. “LA SUCESIÓN DE FIBONACCI EN LA NATURALEZA DE LAS
PLANTAS”, Isagogé, 5 (2008).
[2] Jacques MEYER, « FIBONACCI LEONARDO (1170 env.-env. 1250) », Encyclopædia Universalis [en línea]
[3] Ibid.
[4] Jacques MEYER, « FIBONACCI LEONARDO (1170 env.-env. 1250) », Encyclopædia Universalis [en línea]
[5] Reyes Iglesias, Encarnación. «Arte y Naturaleza en clave geométrica»». Universidad de Valladolid. 2009
[6] Reyes Iglesias, Encarnación. «Arte y Naturaleza en clave geométrica»». Universidad de Valladolid. 2009
[7] Plantes, spirales et nombres, Neuchatel, Universitas Friburgensis, 10/11/2010
[8] Reyes Iglesias, Encarnación. «Arte y Naturaleza en clave geométrica»». Universidad de Valladolid. 2009
[9] Jean-François Morot-Gaudry, Biologie végétale : Croissance et développement, Dunod, 2017
[10] Carlos Segura, Irene Ferrando. « La sucesión de Fibonacci como herramienta para modelizar la naturaleza » Modelling in Science Education and Learning Vol. 3, No. 5, 2010.
[11] “Fibonacci, el matemático que se puso a contar conejos y descubrió la secuencia divina”, BBC News Mundo, 23/02/2019
[12] François Rothen. “Nature : la suite de Fibonacci et les plantes”, Futura Sciences [en línea], 25/02/2019
[13] Carlos Segura, Irene Ferrando. « La sucesión de Fibonacci como herramienta para modelizar la naturaleza » Modelling in Science Education and Learning Vol. 3, No. 5, 2010.
[14] Robert Chalavoux, Nombre d’or, nature et œuvre humaine, Chalagam, 2001
[15] Reyes Iglesias, Encarnación. «Arte y Naturaleza en clave geométrica»». Universidad de Valladolid. 2009
[16] Robert Chalavoux, Nombre d’or, nature et œuvre humaine, Chalagam, 2001